Rabu, 04 Januari 2017

Artikel

FACEBOOK

Kegunaan Facebook Sebagai Media Pembelajaran

A. Sejarah Facebook

Facebook menurut wikipedia berbahasa Indonesia adalah sebuah
layanan jejaring sosial dan situs web yang diluncurkan pada 4 Februari
2004. Facebook didirikan oleh Mark Zuckerberg, seorang mahasiswa
Harvard kelahiran 14 Mei 1984. Pada awal masa kuliahnya, situs jejaring
sosial ini keanggotaannya masih dibatasi untuk mahasiswa dari Harvard
College. Dalam dua bulan selanjutnya, keanggotaannya diperluas ke
sekolah lain di wilayah Boston (Boston College, Universitas Boston,
MIT, Tufts), Rochester, Stanford, NYU,Northwestern, dan semua
sekolah yang termasuk dalam Ivy League. Sampai akhirnya, pada
September 2006, Facebook mulai membuka pendaftaran bagi siapa saja
yang memiliki alamat email dan facebook digunakan banyak orang smua
kalangan dari anak-anak sampai orang dewasa.

Facebook memang digunakan semua kalangan dari anak-anak
maupun orang dewasa. Tetapi pengguna facebook untuk saat ini dipakai
untuk hal-hal yang kurang penting misalnya chating, updat status
maupun game online saja. Khusus untuk remaja dan kaum pelajar, jika
disalahgunakan facebook akan memberi dampak negatif . Adapun
dampak negatif yang daat timbul dari penyalahgunaan facebook antara
lain (1) membuat remaja dan pelajar menjadi malas belajar, tidak
mengerjakan tugas, karena selalu ingin tahu status teman-temannya.(2)
boros, artinya remaja dan pelajar dapat meghabiskan uangnya untuk
online berjam-jam: dan (3) kualitas pertemanan face to facedengan
sesama anggota keluarga semakin berkurang, sehingga menimbulkan
perasaaan terabaikan.

Pengguna facebook tidak hanya memiliki dampak negatif,
penggunaan facebook juga dapat menimbulkan dampak positif. Bahkan,
jika mampu memaksimalkan potensi yang dimiliki facebook, facebook
memiliki potensi dan dampak positif yang lebih besar. Adapun dampak
positif facebook antara lain (1) intraksi dengan jaringan teman-teman
menggunakan email scara internal, berbagai pesan atau informasi secara
private, dan dapat melakukan diskusi secara terbuka; (2) membuat dan
menampilkan status yang mudah diperbaharui; (3) obrolan (chat) scara
langsung; (4) memudahkan dalam memasukkan berbagai video, juga
dapat membuat album foto; (5) dapat dengan mudah menambahkan
konten, juga dapat mengambil beberapa konten yang terdapat pada profil
pengguna lain; (6) memiliki dukungan aplikasi yang luas, baik aplikasi
permainan , hiburan maupun bisnis.

Berdasarkan beberapa dampak positif dari facebook diatas, maka
facebook memiliki potensi besar untuk dapat digunakan dalam dunia
pendidikan dan pembelajaran khusunya untuk media pembelajaran
matematika.

B. Fitur-Fitur Dalam Facebook

Ini adalah beberapa contoh fitur dalam facebook

Status Updates

Fitur ini adalah fitur yang paling dasar digunakan oleh user, yaitu
melakukan posting pesan, baik berupa teks, gambar, link, ataupun
video. Status update ini nantinya dapat dilihat oleh teman-teman yang
ada di facebook, tergantung ada pengaturan yang digunakan.

Sebaliknya teman-teman yang melihat status facebook kita bisa
memberikan komentar atau like ada postingan kita tersebut. Update
status terbaru akan muncul paling atas ditimline dan juga tercatat ada
bagian recently updated ada daftar teman user tersebut.

Message Dan Inbox

Fitur ini digunakan untuk mngirim pesan kepada user lain secara
privat (private Message). User dapat mengirim pesan kepada banyak
teman sekaligus. Namun pesan ini tersimpan dikedua belah pihak,
yaitu pengirim dan penerima. Jika pesan ini dihapus oleh salah satu
pihak, maka pesan tersebut masih ada dipihak yang lain.

Chat/ Obrolan

Untuk saling berbicara dengan pengguna facebook lain melalui tulisan
secara langsung dan real time.

Friends

Fitur ini digunakan oleh facebookers untuk mencari dan mendapatkan
teman, yaitu dengan cara mengetikkan kata pencarian (baik nama
orang, group, berdasarkan lokasi, nama sekolah, dsb), kemudian
mengirimkan permintaan untuk menjadi teman ( sent friend requst).
Kedua facebookers dapat menjadi teman jika pihak yang mndapatkan
requst menyetujuinya. User dapat menolak permintaan tersebut atau
menyembunyikannya dengan menggunakan tombol “not now”

Dinding facbook

Di fitur ini semua konten posting user akan diatur dan ditampilkan
kada orang lain, khususnya teman-teman yang ada di facebook. Di
dinding ini foto, vidoe, dan posting yang ada akan dikatagorikan dan
diurutkan berdasarkan waktu uploadnya (penayangannya). Sehingga
sepintas seperti catatan harian yang mengisikan perjalanan user
tersebut sejak bergabung dngan facebook.

Fitur ini dibuat oleh facebook sebagai sebuah mekanisme atau cara
untuk menyamaikan pesan yang disukai. Kita dapat memberikan like
kada status teman, komentar teman, foto-foto yang di kirim, atau link
yang dikirim oleh teman dll. Cukup dengan menekan tombol like yang
ada dibawah konten tersebut.

News Feeds

Fitur ini merupakan temat dimana aktivitas facebook akan tampil
secara berkala. New feeds ini memberikan informasi seperti
penggantian profil, ulangtahun teman, update status, dan update info
lainnya.

C. Fitur-fitur Facebook sebagai Media Pembelajaran

Banyak fitur yang ditawarkan Facebook sebagai layanan yang
dapat digunakan oleh user dalam rangka memudahkan interaksi. Jika
ditelaah lebih dalam, beberapa diantaranya dapat dimanfaatkan sebagai
media pembelajaran. fitur-fitur tersebut adalah:

Fitur Groups

Layanan situs jejaring sosial Facebook dalam bentuk fitur group
ini memudahkan dalam mengelompokkan sebuah kelas atau mata
pelajaran tertentu. Kelompok yang sudah ada dalam satu group dapat
dengan mudah berdiskusi karena kesamaan tujuan. Selain itu, dengan
adanya fitur group, memudahkan dalam hal koordinasi, dan bertukar
informasi mengenai pelajaran.

Fitur update status dan comment wall-to-wall

Fitur ini merupakan interaksi asynchronous, yaitu interaksi dua arah
secara tidak langsung dimana komunikasi ini akan terdokumentasi
berdasar topik bahasan dan terurut secara waktu.

Fitur note atau docs pada group

Fitur ini sangat memudahkan guru dalam membuat dokumen baru
pada Facebook, baik berupa resume mengenai materi yang sedang
dipelajari atau menyampaikan informasi dengan lebih terstruktur
dan rapi tanpa perlu membuka link baru.

Fitur share link/photo/video

Tujuan dari fitur ini adalah memudahkan user dalam berbagi
informasi. Guru dapat dengan mudah berbagi link/photo/video
yang memuat content mengenai pelajaran yang diampunya. Hal ini
memudahkan murid untuk mendapatkan sumber belajar yang
terpercaya.

Fitur Group Chatting

Aktivitas yang dilakukan pada fitur ini merupakan interaksi dua
arah secara langsung atau yang disebut dengan synchronous yang
terjadi pada sebuah group. Fitur ini merupakan layanan yang paling
memudahkan proses diskusi maupun bertukar informasi dengan cepat
karena anggota group dapat berinteraksi secara langsung dengan
sesama anggota group tersebut yang sedang online.

Tugas Mengurutkan Data

By Unknown 19.30 TUGAS 1 No comments

Mengurutkan Data

Materi Pembelajaran Matematika SMA

By Unknown 19.25 TUGAS 3 No comments

Media Pembelajaran Matematika SMA Kelas XI IPA

Peluang

Aturan perkalian, permutasi dan kombinasi

Masalah yang ada Di Kehidupan Sehari-Hari Di Selesaikan dengan Perbandingan Trigonometri (Mathisfan)

By Unknown 09.27 TUGAS 7 No comments

TRIGONOMETRI

Perbandingan Trogonometri Pada Segitiga Siku-Siku

Perbandingan trigonometri adalah perbandingan sisi-sisi dari segitiga siku-siku. Jadi perbandingan trigonometri hanya berlaku di segitiga siku-siku saja. Bila segitiga itu tidak siku-siku, maka dapatlah kita ubah bentuknya menjadi beberapa segitiga siku-siku.
Perhatikan segitiga siku-siku berikut ini:

Dari segitiga siku-siku diatas didapat perbandingan trigonometri:

\sin α = \frac{sisi depan}{sisi miring} = \frac{b}{a}

\cos α = \frac{sisi samping}{sisi miring} = \frac{c}{a}

\tan α = \frac{sisi depan}{sisi samping} = \frac{b}{c}

cosec α = \frac{1}{\sin α} = \frac{a}{b}

\sec α = \frac{1}{\cos α} = \frac{a}{c}

\cot α = \frac{1}{\tan α} = \frac{c}{b}

Dalam segitiga siku-siku, berlaku pula teori Phytagoras:

a^{2} = b^{2} + c^{2}

b^{2} = a^{2} - c^{2}

c^{2} = a^{2} - b^{2}

Contoh Soal:

1. Tentukan perbandingan trigonometri di sudut

α

Jawab:

\sin α = \frac{12}{13}

\cos α = \frac{5}{13}

\tan α = \frac{12}{5}

cosec α = \frac{13}{12}

\sec α = \frac{13}{5}

\cot α = \frac{5}{12}

2. Diketahui

\sin α = \frac{3}{5}

, tentukan

\cos α

dan

\tan α

Jawab:

t^{2} = 5^{2} - 3^{2}

t^{2} = 25 - 9

t = \sqrt{16}

t = 4

sehingga:

\cos α = \frac{5}{13}

\tan α = \frac{12}{5}

3. Perhatikan gambar dibawah ini:

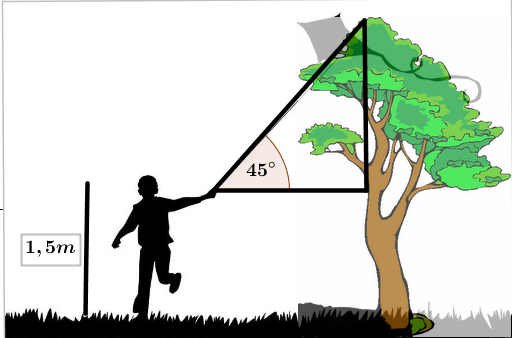
Tentukan tinggi pohon dari gambar diatas, jika diketahui jarak pohon ke manusia sepertiganya tinggi manusia
Jawab:

\cos α = \frac{sisi samping}{sisi miring}

\cos 45^{\circ} = \frac{\frac{1}{2}}{sisi miring}

\cos 45^{\circ} = \frac{\frac{1}{2}}{\frac{1}{2} \sqrt{2}}

sisi miring = 1

sehingga

t^{2} = 1^{2} - (\frac{1}{2})^{2}

t^{2} = 1 - \frac{1}{4}

t^{2} = \frac{3}{4}

t = \frac{1}{2} \sqrt{3}

t = 0,87

jadi, untuk mendapatkan tinggi pohon adalah

t + t manusia = 1,5 + 0,87 = 2,37 m

Membuat Materi Persamaan Lingkaran dengan Menggunakan Mathml dan Geogebra

By Unknown 04.31 TUGAS 6 No comments

PERSAMAAN LINGKARAN

1. Pengertian Lingkaran

Lingkaran adalah tempat kedudukan atau
himpunan titik-titik yang berjarak sama terhadap suatu
titik yang tertentu. Titik tertentu tersebut dinamakan
pusat lingkaran dan jarak yang tetap tersebut dinamakan
jari-jari lingkaran.

Dari gambar di samping, titik O adalah pusat
lingkaran. Titik A, B, C, D terletak pada lingkaran, maka
OA = OB = OC = OD adalah jari-jari lingkaran = r.

2. Persamaan Lingkaran Berpusat di O(0,0) dan (a,b)

a. Persamaan Lingkaran dengan Pusat di O(0, 0)

Jika titik A(xA , yA) terletak pada lingkaran 
yang berpusat di O, maka berlaku OA = jari-jari
lingkaran. Dengan menggunakan rumus jarak titik O(0, 0) 
ke titik A(xA , yA) diperoleh:

 $OA = r = \sqrt{{(x_{A} - 0)}^{2} + {(y_{A} - 0)}^{2}}$

 $r^{2} = {(x_{A} - 0)}^{2} + {(y_{A} - 0)}^{2}$

 $r^{2} = {(x_{A} - 0)}^{2} + {(y_{A} - 0)}^{2}$

Jadi persamaan lingkaran dengan pusat O(0, 0) dan berjari-jari r adalah:

 $x^{2} + y^{2} = r^{2}$

b. Persamaan Lingkaran Berpusat di Titik A(a, b)

Jika titik A(a, b) adalah pusat lingkaran dan titik
B(x, y) terletak pada lingkaran, maka jari-jari
lingkaran r sama dengan jarak dari A ke B.

 $r  =  jarak A ke B$

 $r^{2} = {(AB)}^{2}$

 $r^{2} = {(x_{B} - x_{A})}^{2} + {(y_{B} - y_{A})}^{2}$

 $r^{2} = {(x - a)}^{2} + {(y - b)}^{2}$

Jadi persamaan lingkaran yang berpusat di (a, b) dan berjari-jari r adalah:

 $(x - a)^{2} + (y - b)^{2} = r^{2}$

3. Kedudukan Titik dan Garis terhadap Lingkaran

a. Posisi Titik $P (x_{1}, y_{1}) terhadap Lingkaran x^{2} + y^{2} = r^{2}$

1) Titik $P (x_{1}, y_{1}) terletak di dalam lingkaran,
jika berlaku x^{2} + y^{2} < r^{2}$

2) Titik $P (x_{1}, y_{1}) terletak pada lingkaran,
jika berlaku x^{2} + y^{2} = r^{2}$

3) Titik $P (x_{1}, y_{1}) terletak di luar lingkaran,
jika berlaku x^{2} + y^{2} > r^{2}$

b. Posisi Titik $P (x_{1}, y_{1}) terhadap Lingkaran (x - a)^{2} + (y - b)^{2} = r^{2}$

1) Titik $P (x_{1}, y_{1}) terletak di dalam lingkaran,
jika berlaku (x - a)^{2} + (y - b)^{2} < r^{2}$

2) Titik $P (x_{1}, y_{1}) terletak pada lingkaran,
jika berlaku (x - a)^{2} + (y - b)^{2} = r^{2}$

3) Titik $P (x_{1}, y_{1}) terletak di luar lingkaran,
jika berlaku (x - a)^{2} + (y - b)^{2} > r^{2}$

c. Posisi Garis $g \equiv y = m x + n$ terhadap lingkaran

salah satu cara menentukan kedudukan garis $g \equiv y = m x + n$ terhadap lingkaran $L \equiv x^{2} + y^{2} + A x + B y + C$ dapat diketahui dengan mensubstitusikan persamaan garis g ke lingkaran L, sehingga diperoleh $(1 + m^{2}) x^{2} + (2 mn + A + Bm) x + (n^{2} + Bn + C) = 0$ . persamaan ini adalah persamaan kuadrat dengan tiga kemungkinan diskriminan(D).

1) Garis memotong lingkaran di dua titik, jika D > 0

2) Garis menyinggung lingkaran, jika D = 0

3) Garis diluar lingkaran, jika D < 0

Langkah-Langkah Membuat Lingkaran

1. Buat titik O

2. Buat lingkaran dengan pusat di O dan jari-jari di OA,OB,OC,OD

Langkah-Langkah Membuat Lingkaran dengan Pusat di A(0, 0)

1. Buat titik di A(0,0)

2. Buat lingkaran dengan pusat di A(0,0) dan jari-jari di AB

Langkah-Langkah Membuat Lingkaran Berpusat di Titik A(a, b)

1. Buat titik di A(a,b)

2. Buat lingkaran dengan pusat di A(a,b) dengan jari-jari AB

Langkah-Langkah Membuat Lingkaran Untuk Kedudukan Garis Terhadap Lingkaran

1) Garis Memotong Lingkaran di Dua Titik, jika D>0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b)

3. Buat garis $g \equiv y = m x + n$ di dalam lingkaran yang berpusat dititik A(a,b)

4. tarik garis dari titik A(a,b) yang tegak lurus dengan garis $g \equiv y = m x + n$

2) Garis Menyinggung Lingkaran, jika D=0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b) dan jari-jari di AB

3. Buat garis $g \equiv y = m x + n$ yang menyinggung lingkaran dititik B

3) Garis Di Luar Lingkaran, jika D<0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b) dan jari-jari di AB

3. Buat garis $g \equiv y = m x + n$ diluar lingkaran

Membuat Persamaan Matematika Menggunakan Image

By Unknown 08.19 TUGAS 5 No comments

PERSAMAAN LINGKARAN

LINGKARAN

DEFINISI

lingkaran adalah himpunan titik-titik yang berjarak

sama terhadap sebuah titik tertentu yang disebut pusat lingkaran.

jari-jari lingkaran (r) adalah jarak antara pusat lingkaran dengan

titik pada lingkaran.

Persamaan Lingkaran

Persamaan lingkaran berpusat di O dan berjari-jari r

Persamaan lingkaran di (a,b) dan berjari-jari r

Bentuk umum persamaan lingkaran adalah:

Persamaan Garis Singgung Lingkaran

1. Garis Singgung Lingkaran yang Berpusat di O(0,0)

Persamaan garis singgung di titik(x1,y1) pada

lingkaran adalah:

2. Garis Singgung Lingkaran yang Berpusat di M(a,b) dan Jari-jari r

(i)Persamaan garis singgung di titik (x1,y1) pada

lingkaran yang berpusat di M(a,b)adalah:

(ii)Persamaan garis singgung di titik P(x1,y1) pada

lingkaran yang berpusat M(a,b) dengan jari-jari r adalah:

(iii)persamaan garis singgung dititik P(x1,y1) pada

persamaan umum lingkaran adalah:

3. Garis Singgung Lingkaran Dengan Gradien Tertentu

persamaan garis singgung bergradien m pada lingkaran L

yang berpusat di (a,b) dan jari-jari r adalah:

4. Garis Singgung Dari Suatu Titik di Luar Lingkaran

Persamaan garis singgung lingkaran dengan pusat (a,b),

jari-jari r,dan melalui titik (x,y) adalah:

Rabu, 04 Januari 2017

Kegunaan Facebook Sebagai Media Pembelajaran

A. Sejarah Facebook

B. Fitur-Fitur Dalam Facebook

Ini adalah beberapa contoh fitur dalam facebook

C. Fitur-fitur Facebook sebagai Media Pembelajaran

Mengurutkan Data

Peluang

Aturan perkalian, permutasi dan kombinasi

Kamis, 17 November 2016

Perbandingan Trogonometri Pada Segitiga Siku-Siku

Contoh Soal:

Kamis, 03 November 2016

PERSAMAAN LINGKARAN

1. Pengertian Lingkaran

2. Persamaan Lingkaran Berpusat di O(0,0) dan (a,b)

a. Persamaan Lingkaran dengan Pusat di O(0, 0)

b. Persamaan Lingkaran Berpusat di Titik A(a, b)

3. Kedudukan Titik dan Garis terhadap Lingkaran

a. Posisi Titik P x 1 , y 1 terhadap Lingkaran x 2 + y 2 = r 2

b. Posisi Titik P x 1 , y 1 terhadap Lingkaran ( x - a ) 2 + ( y - b ) 2 = r 2

c. Posisi Garis g ≡ y = m x + n terhadap lingkaran

Langkah-Langkah Membuat Lingkaran

Langkah-Langkah Membuat Lingkaran dengan Pusat di A(0, 0)

Langkah-Langkah Membuat Lingkaran Berpusat di Titik A(a, b)

Langkah-Langkah Membuat Lingkaran Untuk Kedudukan Garis Terhadap Lingkaran

1) Garis Memotong Lingkaran di Dua Titik, jika D>0

2) Garis Menyinggung Lingkaran, jika D=0

3) Garis Di Luar Lingkaran, jika D<0

Rabu, 02 November 2016

LINGKARAN

Persamaan Lingkaran

Persamaan Garis Singgung Lingkaran

1. Garis Singgung Lingkaran yang Berpusat di O(0,0)

2. Garis Singgung Lingkaran yang Berpusat di M(a,b) dan Jari-jari r

3. Garis Singgung Lingkaran Dengan Gradien Tertentu

4. Garis Singgung Dari Suatu Titik di Luar Lingkaran

DAFTAR ISI

Mengenai Saya

Arsip Blog

Labels

Blog Archive

BTemplates.com

Labels

Blogroll

About

a. Posisi Titik $P (x_{1}, y_{1}) terhadap Lingkaran x^{2} + y^{2} = r^{2}$

b. Posisi Titik $P (x_{1}, y_{1}) terhadap Lingkaran (x - a)^{2} + (y - b)^{2} = r^{2}$

c. Posisi Garis $g \equiv y = m x + n$ terhadap lingkaran