Membuat Materi Persamaan Lingkaran dengan Menggunakan Mathml dan Geogebra

PERSAMAAN LINGKARAN

1. Pengertian Lingkaran

Lingkaran adalah tempat kedudukan atau
himpunan titik-titik yang berjarak sama terhadap suatu
titik yang tertentu. Titik tertentu tersebut dinamakan
pusat lingkaran dan jarak yang tetap tersebut dinamakan
jari-jari lingkaran.

Dari gambar di samping, titik O adalah pusat
lingkaran. Titik A, B, C, D terletak pada lingkaran, maka
OA = OB = OC = OD adalah jari-jari lingkaran = r.

2. Persamaan Lingkaran Berpusat di O(0,0) dan (a,b)

a. Persamaan Lingkaran dengan Pusat di O(0, 0)

Jika titik A(xA , yA) terletak pada lingkaran 
yang berpusat di O, maka berlaku OA = jari-jari
lingkaran. Dengan menggunakan rumus jarak titik O(0, 0) 
ke titik A(xA , yA) diperoleh:

$$\text{OA}=\text{r}=\sqrt{{\left(x_A-0\right)}^2+{\left(y_A-0\right)}^2}$$

$${\text{r}}^2={\left(x_A-0\right)}^2+{\left(y_A-0\right)}^2$$

$${\text{r}}^2={\left(x_A-0\right)}^2+{\left(y_A-0\right)}^2$$

Jadi persamaan lingkaran dengan pusat O(0, 0) dan berjari-jari r adalah:

$$x^2+y^2=r^2$$

b. Persamaan Lingkaran Berpusat di Titik A(a, b)

Jika titik A(a, b) adalah pusat lingkaran dan titik
B(x, y) terletak pada lingkaran, maka jari-jari
lingkaran r sama dengan jarak dari A ke B.

$$\mathrm{r\; =\; jarak\; A\; ke\; B}$$

$$r^2={\left(AB\right)}^2$$

$$r^2={\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2$$

$$r^2={\left(x-a\right)}^2+{\left(y-b\right)}^2$$

Jadi persamaan lingkaran yang berpusat di (a, b) dan berjari-jari r adalah:

$$(x-a{)}^2+(y-b{)}^2=r^2$$

3. Kedudukan Titik dan Garis terhadap Lingkaran

a. Posisi Titik P\left(x_1,y_1\right)terhadap\; Lingkaran{x}^2+y^2=r^2

1) Titik P\left(x_1,y_1\right)terletak\; di\; dalam\; lingkaran,\; jika\; berlaku{x}^2+y^2<r^2

2) Titik P\left(x_1,y_1\right)terletak\; pada\; lingkaran,\; jika\; berlaku{x}^2+y^2=r^2

3) Titik P\left(x_1,y_1\right)terletak\; di\; luar\; lingkaran,\; jika\; berlaku{x}^2+y^2>r^2

b. Posisi Titik P\left(x_1,y_1\right)terhadap\; Lingkaran(x-a{)}^2+(y-b{)}^2=r^2

1) Titik P\left(x_1,y_1\right)terletak\; di\; dalam\; lingkaran,\; jika\; berlaku(x-a{)}^2+(y-b{)}^2<r^2

2) Titik P\left(x_1,y_1\right)terletak\; pada\; lingkaran,\; jika\; berlaku(x-a{)}^2+(y-b{)}^2=r^2

3) Titik P\left(x_1,y_1\right)terletak\; di\; luar\; lingkaran,\; jika\; berlaku(x-a{)}^2+(y-b{)}^2>r^2

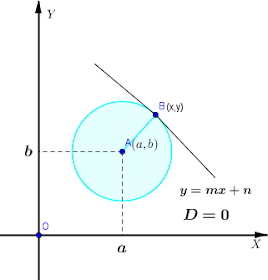
c. Posisi Garis g\equiv y=mx+n terhadap lingkaran

salah satu cara menentukan kedudukan garis g\equiv y=mx+n terhadap lingkaran L\equiv x^2+y^2+Ax+By+C dapat diketahui dengan mensubstitusikan persamaan garis g ke lingkaran L, sehingga diperoleh (1+m^2)x^2+(2mn+A+Bm)x+(n^2+Bn+C)=0. persamaan ini adalah persamaan kuadrat dengan tiga kemungkinan diskriminan(D).

1) Garis memotong lingkaran di dua titik, jika D > 0

2) Garis menyinggung lingkaran, jika D = 0

3) Garis diluar lingkaran, jika D < 0

Langkah-Langkah Membuat Lingkaran

1. Buat titik O

2. Buat lingkaran dengan pusat di O dan jari-jari di OA,OB,OC,OD

Langkah-Langkah Membuat Lingkaran dengan Pusat di A(0, 0)

1. Buat titik di A(0,0)

2. Buat lingkaran dengan pusat di A(0,0) dan jari-jari di AB

Langkah-Langkah Membuat Lingkaran Berpusat di Titik A(a, b)

1. Buat titik di A(a,b)

2. Buat lingkaran dengan pusat di A(a,b) dengan jari-jari AB

Langkah-Langkah Membuat Lingkaran Untuk Kedudukan Garis Terhadap Lingkaran

1) Garis Memotong Lingkaran di Dua Titik, jika D>0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b)

3. Buat garis g\equiv y=mx+n di dalam lingkaran yang berpusat dititik A(a,b)

4. tarik garis dari titik A(a,b) yang tegak lurus dengan garis g\equiv y=mx+n

2) Garis Menyinggung Lingkaran, jika D=0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b) dan jari-jari di AB

3. Buat garis g\equiv y=mx+n yang menyinggung lingkaran dititik B

3) Garis Di Luar Lingkaran, jika D<0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b) dan jari-jari di AB

3. Buat garis g\equiv y=mx+n diluar lingkaran