Masalah yang ada Di Kehidupan Sehari-Hari Di Selesaikan dengan Perbandingan Trigonometri (Mathisfan)

Perbandingan Trogonometri Pada Segitiga Siku-Siku

Perbandingan trigonometri adalah perbandingan sisi-sisi dari segitiga siku-siku. Jadi perbandingan trigonometri hanya berlaku di segitiga siku-siku saja. Bila segitiga itu tidak siku-siku, maka dapatlah kita ubah bentuknya menjadi beberapa segitiga siku-siku.
Perhatikan segitiga siku-siku berikut ini:

Dari segitiga siku-siku diatas didapat perbandingan trigonometri:
\sin \alpha =\frac{\mathrm{sisi\; depan}}{\mathrm{sisi\; miring}}=\frac{b}{a}
\cos \alpha =\frac{\mathrm{sisi\; samping}}{\mathrm{sisi\; miring}}=\frac{c}{a}
\tan \alpha =\frac{\mathrm{sisi\; depan}}{\mathrm{sisi\; samping}}=\frac{b}{c}
\mathrm{cosec}\alpha =\frac{1}{\sin \alpha }=\frac{a}{b}
\sec \alpha =\frac{1}{\cos \alpha }=\frac{a}{c}
\cot \alpha =\frac{1}{\tan \alpha }=\frac{c}{b}
Dalam segitiga siku-siku, berlaku pula teori Phytagoras:
a^2=b^2+c^2
b^2=a^2-c^2
c^2=a^2-b^2

Contoh Soal:

1. Tentukan perbandingan trigonometri di sudut \alpha:

Jawab:
\sin \alpha =\frac{12}{13}
\cos \alpha =\frac{5}{13}
\tan \alpha =\frac{12}{5}
\mathrm{cosec}\alpha =\frac{13}{12}
\sec \alpha =\frac{13}{5}
\cot \alpha =\frac{5}{12}
2. Diketahui \sin \alpha =\frac{3}{5}, tentukan \cos \alpha dan \tan \alpha
Jawab:

t^2=5^2-3^2
t^2=25-9
t=\sqrt{16}
t=4
sehingga:
\cos \alpha =\frac{5}{13}
\tan \alpha =\frac{12}{5}
3. Perhatikan gambar dibawah ini:

Tentukan tinggi pohon dari gambar diatas, jika diketahui jarak pohon ke manusia sepertiganya tinggi manusia
Jawab:
\cos \alpha =\frac{\mathrm{sisi\; samping}}{\mathrm{sisi\; miring}}
\cos {\mathrm{45}}^{\circ }=\frac{\frac{1}{2}}{\mathrm{sisi\; miring}}
\cos {\mathrm{45}}^{\circ }=\frac{\frac{1}{2}}{\frac{1}{2}\sqrt{2}}
\mathrm{sisi\; miring}=1
sehingga

t^2=1^2-(\frac{1}{2}{)}^2
t^2=1-\frac{1}{4}
t^2=\frac{3}{4}
t=\frac{1}{2}\sqrt{3}
t=\mathrm{0,87}
jadi, untuk mendapatkan tinggi pohon adalah
t+\mathrm{t\; manusia}=\mathrm{1,5}+\mathrm{0,87}=\mathrm{2,37}m

Membuat Materi Persamaan Lingkaran dengan Menggunakan Mathml dan Geogebra

PERSAMAAN LINGKARAN

1. Pengertian Lingkaran

Lingkaran adalah tempat kedudukan atau
himpunan titik-titik yang berjarak sama terhadap suatu
titik yang tertentu. Titik tertentu tersebut dinamakan
pusat lingkaran dan jarak yang tetap tersebut dinamakan
jari-jari lingkaran.

Dari gambar di samping, titik O adalah pusat
lingkaran. Titik A, B, C, D terletak pada lingkaran, maka
OA = OB = OC = OD adalah jari-jari lingkaran = r.

2. Persamaan Lingkaran Berpusat di O(0,0) dan (a,b)

a. Persamaan Lingkaran dengan Pusat di O(0, 0)

Jika titik A(xA , yA) terletak pada lingkaran 
yang berpusat di O, maka berlaku OA = jari-jari
lingkaran. Dengan menggunakan rumus jarak titik O(0, 0) 
ke titik A(xA , yA) diperoleh:

$$\text{OA}=\text{r}=\sqrt{{\left(x_A-0\right)}^2+{\left(y_A-0\right)}^2}$$

$${\text{r}}^2={\left(x_A-0\right)}^2+{\left(y_A-0\right)}^2$$

$${\text{r}}^2={\left(x_A-0\right)}^2+{\left(y_A-0\right)}^2$$

Jadi persamaan lingkaran dengan pusat O(0, 0) dan berjari-jari r adalah:

$$x^2+y^2=r^2$$

b. Persamaan Lingkaran Berpusat di Titik A(a, b)

Jika titik A(a, b) adalah pusat lingkaran dan titik
B(x, y) terletak pada lingkaran, maka jari-jari
lingkaran r sama dengan jarak dari A ke B.

$$\mathrm{r\; =\; jarak\; A\; ke\; B}$$

$$r^2={\left(AB\right)}^2$$

$$r^2={\left(x_B-x_A\right)}^2+{\left(y_B-y_A\right)}^2$$

$$r^2={\left(x-a\right)}^2+{\left(y-b\right)}^2$$

Jadi persamaan lingkaran yang berpusat di (a, b) dan berjari-jari r adalah:

$$(x-a{)}^2+(y-b{)}^2=r^2$$

3. Kedudukan Titik dan Garis terhadap Lingkaran

a. Posisi Titik P\left(x_1,y_1\right)terhadap\; Lingkaran{x}^2+y^2=r^2

1) Titik P\left(x_1,y_1\right)terletak\; di\; dalam\; lingkaran,\; jika\; berlaku{x}^2+y^2<r^2

2) Titik P\left(x_1,y_1\right)terletak\; pada\; lingkaran,\; jika\; berlaku{x}^2+y^2=r^2

3) Titik P\left(x_1,y_1\right)terletak\; di\; luar\; lingkaran,\; jika\; berlaku{x}^2+y^2>r^2

b. Posisi Titik P\left(x_1,y_1\right)terhadap\; Lingkaran(x-a{)}^2+(y-b{)}^2=r^2

1) Titik P\left(x_1,y_1\right)terletak\; di\; dalam\; lingkaran,\; jika\; berlaku(x-a{)}^2+(y-b{)}^2<r^2

2) Titik P\left(x_1,y_1\right)terletak\; pada\; lingkaran,\; jika\; berlaku(x-a{)}^2+(y-b{)}^2=r^2

3) Titik P\left(x_1,y_1\right)terletak\; di\; luar\; lingkaran,\; jika\; berlaku(x-a{)}^2+(y-b{)}^2>r^2

c. Posisi Garis g\equiv y=mx+n terhadap lingkaran

salah satu cara menentukan kedudukan garis g\equiv y=mx+n terhadap lingkaran L\equiv x^2+y^2+Ax+By+C dapat diketahui dengan mensubstitusikan persamaan garis g ke lingkaran L, sehingga diperoleh (1+m^2)x^2+(2mn+A+Bm)x+(n^2+Bn+C)=0. persamaan ini adalah persamaan kuadrat dengan tiga kemungkinan diskriminan(D).

1) Garis memotong lingkaran di dua titik, jika D > 0

2) Garis menyinggung lingkaran, jika D = 0

3) Garis diluar lingkaran, jika D < 0

Langkah-Langkah Membuat Lingkaran

1. Buat titik O

2. Buat lingkaran dengan pusat di O dan jari-jari di OA,OB,OC,OD

Langkah-Langkah Membuat Lingkaran dengan Pusat di A(0, 0)

1. Buat titik di A(0,0)

2. Buat lingkaran dengan pusat di A(0,0) dan jari-jari di AB

Langkah-Langkah Membuat Lingkaran Berpusat di Titik A(a, b)

1. Buat titik di A(a,b)

2. Buat lingkaran dengan pusat di A(a,b) dengan jari-jari AB

Langkah-Langkah Membuat Lingkaran Untuk Kedudukan Garis Terhadap Lingkaran

1) Garis Memotong Lingkaran di Dua Titik, jika D>0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b)

3. Buat garis g\equiv y=mx+n di dalam lingkaran yang berpusat dititik A(a,b)

4. tarik garis dari titik A(a,b) yang tegak lurus dengan garis g\equiv y=mx+n

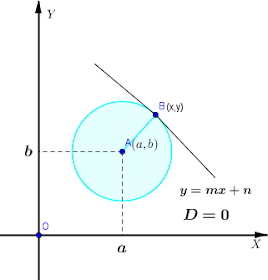
2) Garis Menyinggung Lingkaran, jika D=0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b) dan jari-jari di AB

3. Buat garis g\equiv y=mx+n yang menyinggung lingkaran dititik B

3) Garis Di Luar Lingkaran, jika D<0

1. Buat Titik di A(a,b)

2. Buat lingkaran dengan pusat di Titik A(a, b) dan jari-jari di AB

3. Buat garis g\equiv y=mx+n diluar lingkaran

Membuat Persamaan Matematika Menggunakan Image

LINGKARAN

DEFINISI

lingkaran adalah himpunan titik-titik yang berjarak

sama terhadap sebuah titik tertentu yang disebut pusat lingkaran.

jari-jari lingkaran (r) adalah jarak antara pusat lingkaran dengan

titik pada lingkaran.

Persamaan Lingkaran

Persamaan lingkaran berpusat di O dan berjari-jari r

Persamaan lingkaran di (a,b) dan berjari-jari r

Bentuk umum persamaan lingkaran adalah:

Persamaan Garis Singgung Lingkaran

1. Garis Singgung Lingkaran yang Berpusat di O(0,0)

Persamaan garis singgung di titik(x1,y1) pada

lingkaran adalah:

2. Garis Singgung Lingkaran yang Berpusat di M(a,b) dan Jari-jari r

(i)Persamaan garis singgung di titik (x1,y1) pada

lingkaran yang berpusat di M(a,b)adalah:

(ii)Persamaan garis singgung di titik P(x1,y1) pada

lingkaran yang berpusat M(a,b) dengan jari-jari r adalah:

(iii)persamaan garis singgung dititik P(x1,y1) pada

persamaan umum lingkaran adalah:

3. Garis Singgung Lingkaran Dengan Gradien Tertentu

persamaan garis singgung bergradien m pada lingkaran L 

yang berpusat di (a,b) dan jari-jari r adalah:

4. Garis Singgung Dari Suatu Titik di Luar Lingkaran

Persamaan garis singgung lingkaran dengan pusat (a,b),

jari-jari r,dan melalui titik (x,y) adalah:

Membuat Persamaan Matematika Menggunakan Mathml

LINGKARAN

DEFINISI
lingkaran adalah himpunan titik-titik yang berjarak sama terhadap sebuah titik tertentu yang disebut pusat lingkaran.
jari-jari lingkaran (r) adalah jarak antara pusat lingkaran dengan titik pada lingkaran.

Persamaan Lingkaran

Persamaan lingkaran berpusat di O dan berjari-jari r

$$x^2+y^2=r^2$$

Persamaan lingkaran di (a,b) dan berjari-jari r

$$(x-a{)}^2+(y-b{)}^2=r^2$$

Bentuk umum persamaan lingkaran adalah:

$$x^2+y^2+Ax+By+C=0$$

Persamaan Garis Singgung Lingkaran

1. Garis Singgung Lingkaran yang Berpusat di O(0,0)

Persamaan garis singgung di titik(x1,y1)

pada lingkaran adalah:

$$x{x}_1+y{y}_1=r^2$$

2. Garis Singgung Lingkaran yang Berpusat di M(a,b)dan Jari-jari r

(i)Persamaan garis singgung di titik (x1,y1)

pada lingkaran yang berpusat di M(a,b)adalah:

$$(y-y_1)(y_1-b)=-(x-x_1)(x_1-a)$$

(ii)Persamaan garis singgung di titik P(x1,y1)

pada lingkaran yang berpusat M(a,b) dengan

jari-jari r adalah:

$$(x-a)(x_1-a)+(y-b)(y_1-b)=r^2$$ 

(iii) persamaan garis singgung dititik P(x1,y1)

pada persamaan umum lingkaran adalah:

$$x{x}_1+y{y}_1+\frac{1}{2}A(x+x_1)+\frac{1}{2}B(y+y_1)+C=0$$

3. Garis Singgung Lingkaran Dengan Gradien Tertentu

persamaan garis singgung bergradien m pada

lingkaran L yang berpusat di (a,b) dan

jari-jari r adalah:

$$y-b=m(x-a)+r\sqrt{1+m^2}atauy-b=m(x-a)-r\sqrt{1+m^2}$$

4. Garis Singgung Dari Suatu Titik di Luar Lingkaran

Persamaan garis singgung lingkaran dengan pusat (a,b),

jari-jari r,dan melalui titik (x,y) adalah:

$$y-y_1=m(x-x_1)$$
$$m=\frac{(y_1-b)(x_1-a)\pm \sqrt{(y_1-b{)}^2+(x_1-a{)}^2-r^2}}{(x_1-a{)}^2-{\text{r}}^2}$$